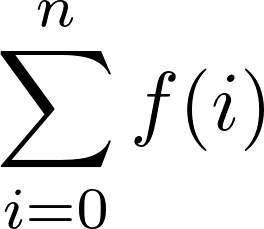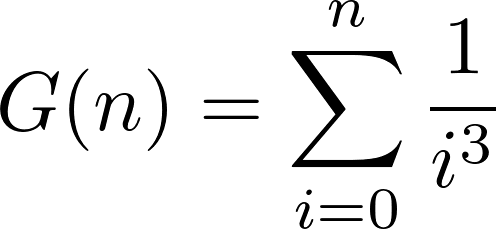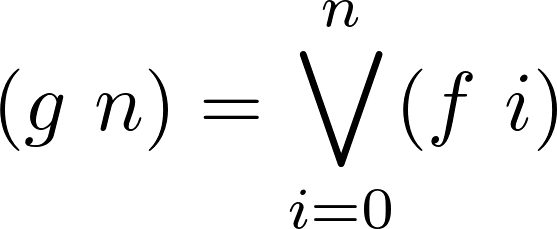Programación 1 - Práctica 6
1 Números Naturales
1.1 Introducción
DrRacket provee muchas funciones que consumen listas y algunas pocas que producen listas. Entre estas últimas se encuentra la función make-list que toma un valor n y otro v para devolver una lista de tamaño n que contiene a v como único valor.
Aquí podemos ver algunos ejemplos:
> (make-list 2 "hello") (cons "hello" (cons "hello" '())) > (make-list 3 #true) (cons #true (cons #true (cons #true '()))) > (make-list 0 17) '()
En resumen, aunque esta función consume sólo datos atómicos, permite construir datos arbitrariamente grandes. ¿Cómo es esto posible?
La respuesta a esa pregunta es que el primer argumento de make-list no es cualquier número sino que es un tipo especial de número. En ciencias de la computación los llamamos "números naturales", son aquellos que nos permiten contar.
Los números naturales tienen su propia definición de tipo:
; Un Natural es: ; – 0 ; – (add1 Natural) ; interpretación: Natural representa los números naturales
Como puede ver, esta definición es una definición autoreferenciada similar a la que usamos cuando definimos listas.
Miremos de cerca la definición de números naturales:
La primera cláusula nos dice que 0 es un número natural; en este caso indica que no hay objetos que puedan ser contados. La segunda cláusula dice que si n es un número natural, entonces (add1 n) también lo es. Ya que add1 es una función que suma 1 a cualquier número, podríamos reescribir esta segunda cláusula como (+ n 1), pero usamos add1 para indicar que esta suma es especial.
Lo que tiene de especial el uso de add1 es que actúa como un constructor. Por esta razón, DrRacket provee también la función sub1, que es el "selector" correspondiente a add1. Dado un número natural m distinto de 0, podemos usar sub1 para averiguar el número que se usó para la construcción de m. En otras palabras sub1 devuelve el predecesor de un número natural positivo
Los predicados que se usan para identificar el 0 y el resto de los números naturales son zero? y positive?, respectivamente.
A partir de ahora, podemos construir funciones que tomen como argumentos números naturales. Definamos por nuestra cuenta la función copiar que se comporta como make-list:
Notar que la aplicación sucesiva de add1 sobre 0 nos permite contruir todos los naturales: (add1 0)=1, (add1 (add1 0))=2, etc. Es por eso que para simplificar la escritura vamos a utilizar los valores 1, 2, 3, 4, ... para representar los números naturales
; copiar: Natural String -> Lista(String) ; El propósito de la función copiar es crear una lista de ; n copias de una cadena s (check-expect (copiar 2 "hola") (list "hola" "hola")) (check-expect (copiar 0 "hola") '()) (check-expect (copiar 4 "abc") (list "abc" "abc" "abc" "abc"))
Una vez que tenemos clara la signatura, el propósito de la función y algunos ejemplos concretos que muestran el comportamiento deseado, debemos definir la función. La función copiar deberá analizar si el número natural que se pasa como entrada es el 0 o si es un número positivo.
Así, el cuerpo de la función tendrá una expresión cond con dos cláusulas:
(define (copiar n s) (cond [(zero? n) '()] [(positive? n) (cons s (copiar (sub1 n) s))]))
Si la entrada es 0 eso significa que se debe producir una lista con 0 elementos. Por otro lado, según la declaración de propósito de copiar, lo que produce (copiar (sub1 n) s) es un lista con n-1 copias de s, por lo tanto, para calcular (copiar n s) faltaría únicamente agregar una copia de s a dicho resultado. Esto se logra haciendo (cons s (copiar (sub1 n) s)).
Operador |
| Tipo de Operador |
| Función |
0 |
| Constructor |
| Constante usada para representar el primer número natural |
add1 |
| Constructor |
| Calcula el sucesor de un número natural |
sub1 |
| Selector |
| Devuelve el predecesor de un número natural positivo |
zero? |
| Predicado |
| Reconoce al natural 0 |
positive? |
| Predicado |
| Reconoce naturales construidos con add1 |
Ahora que tenemos en claro la definición de números naturales, vamos a practicar!
1.2 Ejercitación
Ejercicio 1. Diseñe la función sumanat que toma dos números naturales y sin usar + devuelve un natural que es la suma de ambos. Use el evaluador paso a paso para evaluar (sumanat 3 2).
Ejercicio 2. Diseñe la función multiplicar. Esta función debe tomar como entrada dos números naturales y debe multiplicarlos sin usar * ni +. Use el evaluador paso a paso para evaluar (multiplicar 3 2). Puede utilizar el ejercicio anterior.
Ejercicio 3. Diseñe la función powernat que toma dos números naturales y devuelve el resultado de elevar el primero a la potencia del segundo, usando la función multiplicar definida en el ejercicio anterior. Use el evaluador paso a paso para evaluar (powernat 4 2).
Ejercicio 4. Diseñe una función sigma: Natural (Natural -> Number) -> Number, que dados un número natural n y una función f, devuelve la sumatoria de f para los valores de 0 hasta n. Es decir, calcular:
(check-expect (sigma 4 sqr) 30) (check-expect (sigma 10 identity) 55)
Ejercicio 5. A partir del ejercicio anterior, es posible calcular sumatorias que encontramos frecuentemente en los cursos de matemática. Por ejemplo, si quisiéramos calcular
sólo debemos concentrarnos en definir una función que calcule el recíproco del cubo de un número natural. Luego combinamos esta función con la función sigma definida en el ejercicio anterior y podemos definir G fácilmente.
Siguiendo esta idea, programe las funciones R, S y T definidas como sigue:
Observación: Como no conocemos el propósito de estas funciones, sólo pedimos que para las mismas dé sus signaturas, casos de prueba y definición.
Atención: Para los casos de test, quizás le convenga explorar la función check-within, que es útil para realizar testing con valores no exactos.
Ejercicio 6. Diseñe la función intervalo, que dado un número natural n, devuelve la lista (list 1 2 ... n). Para 0 devuelve '().
Ayuda: Quizás le convenga devolver la lista en orden descendente. Luego la función reverse lo resuelve fácilmente.
Ejercicio 7. Diseñe la función factnat que toma un número natural y devuelve su factorial. El factorial de un número natural n se calcula haciendo 1 x 2 x ... x n. Use el evaluador paso a paso para evaluar (factnat 4).
Ejercicio 8. Diseñe la función fibnat que toma un número natural y devuelve el valor correspondiente a la secuencia de Fibonacci para ese valor:
fibnat (0) = 1
fibnat (1) = 1
fibnat (n+2) = fibnat (n) + fibnat (n+1)
Use el evaluador paso a paso para calcular (fibnat 5).
Ejercicio 9. Diseñe una función list-fibonacci que dado un número n devuelve una lista con los primeros n+1 valores de la serie de fibonacci, ordenados de mayor a menor. Es decir, (list-fibonacci n) = (list (fib n) (fib (- n 1)) ... (fib 0))
(check-expect (list-fibonacci 4) (list 5 3 2 1 1)) (check-expect (list-fibonacci 0) (list 1))
g (0) = 1
g (1) = 2
g (2) = 3
g (n) = g (n-1) * g (n-2) * g (n-3) para todo n mayor o igual a 3
Diseñe una función list-g que dado un número n devuelve la lista con los valores que resulta de evaluar a g en n, n-1, n-2,...,0. Es decir (list-g n) = (list (g n) (g (- 1 n)) ... (g 1) (g 0)).
(check-expect (list-g 4) (list 36 6 3 2 1)) (check-expect (list-g 0) (list 1))
una función f: Number -> Number,
un natural n, y
un número x,
Por ejemplo:
(check-expect (componer sqr 2 5) 625) (check-expect (componer add1 5 13) 18)
Presente al menos dos ejemplos más en su diseño.
Ejercicio 12. Diseñe una función multiplos que tome dos naturales n y m, y devuelva una lista con los primeros n múltiplos positivos de m, en orden inverso: m * n, m * (n-1), ... , m * 2, m.
Por ejemplo:
(check-expect (multiplos 4 7) (list 28 21 14 7)) (check-expect (multiplos 0 11) '())
Ejercicio 13. Estamos interesados en definir una función g que dado un número natural n y una función f: Natural -> Boolean, devuelve #true si y sólo si alguno de los valores (f 0) ,(f 1) ,... (f n) es #true.
Por ejemplo:
(check-expect (g 3 negative?) #false) (check-expect (g 7 even?) #true)
En lógica, suele usarse el símbolo ![]() para representar el operador
or. Podemos expresar g de la siguiente manera:
para representar el operador
or. Podemos expresar g de la siguiente manera:
Diseñe la función g.
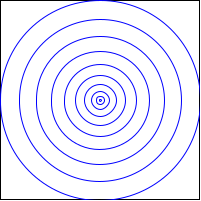
Ejercicio 14. Diseñe una función circulos que tome un número natural m y devuelva una imagen cuadrada de lado 2*m2 con m círculos azules centrados y radios: m2, (m-1)2, ... , 22, 1 respectivamente.
Por ejemplo:
(circulos 10) =
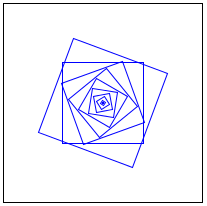
Ejercicio 15. Diseñe una función cuadrados que tome un número natural m, un ángulo ang y devuelva una imagen cuadrada de lado 200 con m cuadrados azules centrados. Los cuadrados azules tendrán lados de tamaño: m2, (m-1)2, ... , 22,1 respectivamente. El ángulo ang indica la rotación del cuadrado de mayor dimensión. El ángulo que corresponde al cuadrado de lado (m-1)2 debe ser de 20 grados mayor que el que le corresponde al cuadrado de lado m2, para cualquier valor de m mayor o igual a 1.
Por ejemplo:
(cuadrados 10 70) =
la parte correspondiente a la devolución del préstamo, que se calcula así: total/n;
la parte correspondiente a los intereses de la cuota, que se calcula así: (total/n) * (i/ (100*12)) * j.
Diseñe una función cuotas que dado un importe total de un préstamo, un valor n correspondiente al número de cuotas, una tasa i de interés, devuelva una lista con las cuotas a pagar ordenadas de forma creciente.
(check-expect (cuotas 10000 0 18) '()) (check-expect (cuotas 10000 1 12) (list 10100)) (check-expect (cuotas 30000 3 12) (list 10100 10200 10300)) (check-expect (cuotas 100000 4 18) (list 25375 25750 26125 26500))