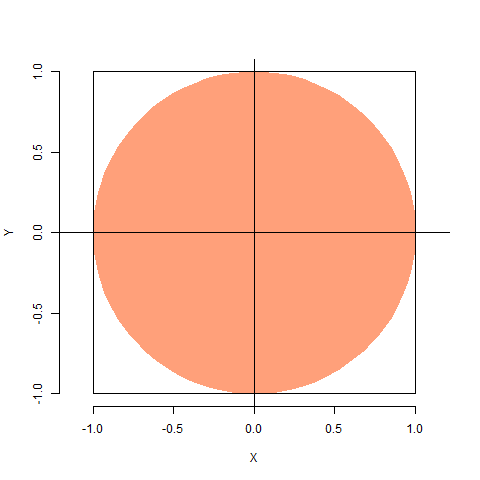Programación 1 - Práctica 7, primera parte
1 Experimentos aleatorios
Ejercicio 1. Según la profesora de probabilidad y estadística, al tirar muchas veces un dado -si este no está cargado- la frecuencia con la que ocurre cada número tiende a ser la misma. Es decir, si tiramos un dado de seis caras doce millones de veces y anotamos los resultados, es de esperar que cada número del 1 al 6 aparezca aproximadamente dos millones de veces.
(define CARAS 6)
Diseñe una función simular-dado, que reciba un número natural n y devuelva una lista con n números aleatorios entre 1 y CARAS.
(define MAX 60000) (define EXPERIMENTO (simular-dado MAX)) (define VALORES (intervalo CARAS))
Diseñe la función frecuencia, que dado un número natural n y una lista de naturales, devuelve la cantidad de veces que n aparece en la lista. Es decir, su frecuencia absoluta.
(define (frecuencia-relativa n l) (/ (frecuencia n l) (length l)))
(define (frec-rel-exp n) (frecuencia-relativa n EXPERIMENTO))
Usando map, podemos calcular las frecuencias relativas de cada valor en el experimento:
(define FRECUENCIAS-RELATIVAS (map frec-rel-exp VALORES))
¿Qué valor aproximado debería repetirse en la lista FRECUENCIAS-RELATIVAS? Antes de proceder a evaluar en DrRacket, piense. Luego, evalúe.
Experimente con diferentes valores para MAX. Para estar más cerca del valor esperado, ¿MAX debe ser más grande o más chico?
¿Qué pasa si usamos 2 para el valor de CARAS? ¿Qué frecuencias relativas deberíamos esperar? ¿Qué experimento estaríamos simulando?
Repita las preguntas del ítem anterior, pero con CARAS = 37.
Considere ahora que el experimento es tirar dos dados de seis caras. En este caso, la frecuencia esperada para cada resultado posible no es la misma. Diseñe un programa que calcule las frecuencias relativas de todos los posibles valores del experimento, tomando como base el programa de más arriba. Los cambios no deberían ser muchos.
2 El método de Montecarlo
El Método de Montecarlo es un método numérico estadístico, usado para aproximar expresiones matemáticas. En general, este método se usa cuando obtener una solución exacta es imposible o muy costoso computacionalmente.
En esta práctica lo utilizaremos para aproximar valores y calcular áreas o volúmenes, aunque tiene muchas otras aplicaciones a la física, la matemática y la economía, destacándose sus aplicaciones en teoría de juegos.
2.1 Aproximando áreas
Consideremos la siguiente figura:
Imaginemos que queremos estimar el área del círculo sombreado. El método Montecarlo nos sugiere lo siguiente:
Coloquemos la figura cuya área queremos estimar dentro de otra cuya área sea conocida. En este caso, tomamos el cuadrado de lado 2 (y área 4).
Generemos de forma aleatoria un punto dentro del cuadrado, y anotemos si este punto cae dentro de la figura. Repitamos este experimento un gran número de veces.
Como la probabilidad que uno de los puntos generados caiga dentro de la figura es proporcional a su área, podemos realizar la siguiente estimación, calculando la proporción de puntos que cayeron dentro:
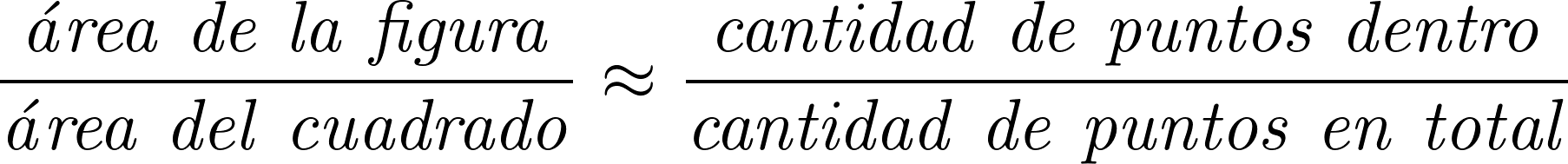
Despejando:
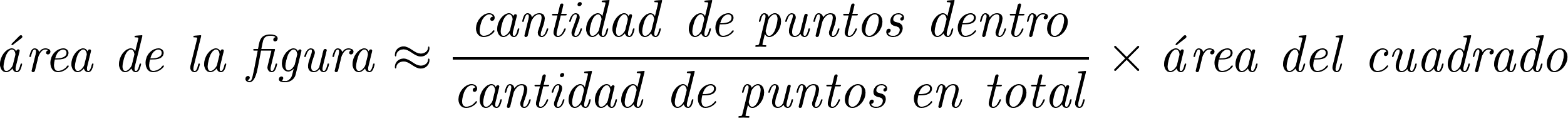
El archivo montecarlo-pi.rkt tiene un programa que implementa estas ideas para calcular el área del círculo de la figura.
2.2 Más estimaciones con círculos
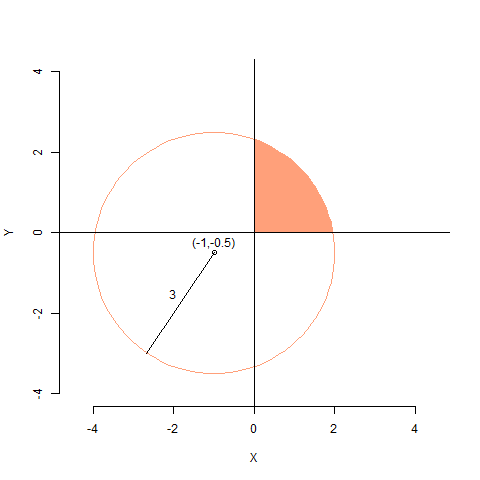
Modifique el programa anterior para calcular el área sombreada en la siguiente figura:
El círculo está centrado en el punto (-1 ,-0.5), y tiene radio 3. Observe que en este caso no es tan sencillo predecir cuál es el resultado. Los cambios al programa original deberían ser muy pequeños. Piense primero en qué cuadrado inscribirá el área sombreada. No hace falta que contenga al círculo, sólo es necesario que contenga la superficie cuya área queremos aproximar.
3 Números primos
Decimos que un número natural n mayor o igual que 2 es primo si sus únicos divisores positivos son 1 y n. Los números que no son primos se llaman compuestos. El Teorema fundamental de la aritmética nos dice que todo número entero positivo o bien es primo, o bien puede expresarse como el producto de números primos de forma única. Hace más de 2000 años Euclides demostró que existen infinitos números primos.
Determinar si un número arbitrario n es primo es un problema computacionalmente difícil para grandes valores de n. En la dificultad de este problema basan su seguridad muchos algoritmos de encriptación. Por ejemplo, el popular sistema de criptografía de clave pública-privada RSA.
3.1 La Criba de Eratóstenes
En el siglo III antes de Cristo, el filósofo Eratóstenes describió un método para encontrar todos los números primos hasta un número predeterminado n.
Se marca el primer elemento -llamémosle k- como número primo.
Se borran todos los múltiplos de k de la lista (salvo k).
Una vez finalizado este procedimiento, tenemos la garantía que los números que quedaron marcados son todos los números primos entre 2 y n.
Diseñe una función criba-eratostenes, que dado un natural n, devuelva una lista con todos los primos menores o iguales que n siguiendo el procedimiento descripto. El archivo eratostenes-subir.rkt puede servir como guía, aunque también se puede arrancar desde el principio.
Para utilizar las funciones que operan sobre archivos debe cargar el paquete de enseñanza batch-io.
3.2 Verificando primalidad
La criba de eratóstenes nos permite generar una lista con todos los primos hasta un cierto número. Sin embargo, muchas veces sólo necesitamos verificar si un número m es primo o compuesto. Si bien podríamos generar la criba de eratóstenes hasta m y luego ver si m quedó sin tachar (y por lo tanto es primo), esto puede resultar computacionalmente costoso, y debemos buscar otra alternativa.
Como vimos en clase, y es conocido desde hace siglos, si m no tiene divisores menores o iguales que
entonces es primo.
Las funciones read-file y/o read-csv-file pueden ser de utilidad.
(define MAX 10000) (define LISTA-DE-PRIMOS ....)
Un número 
es primo si y sólo si no
tiene algún divisor en LISTA-DE-PRIMOS. Observe que podemos entonces
determinar la primalidad de números hasta 100.000.000 construyendo la criba sólo hasta 10.000.
Diseñe un predicado es-primo? que dado un nátural m menor o igual que 
determine si este es primo o compuesto.
Generalice el diseño anterior mediante una función todos-primos?, que dada una lista de números menores o iguales
a , determine si todos ellos son primos. Para los casos de test, tal vez le interese saber que
86077909, 96928157, 49987169 y 54257153 son primos (debería ser más sencillo encontrar ejemplos de números que no lo son).
4 Criptografía
La Criptografía se encarga del estudio de técnicas para intercambiar información de forma segura frente a la presencia de terceras partes (llamadas normalmente adversarios). Es un área importante y con muchas aplicaciones dentro de las ciencias de la computación, en particular en lo referido a seguridad informática.
4.1 El cifrado del César
El Cifrado del César es un mecanismo de criptografía simétrica muy simple, en la cual el emisor y el receptor utilizan una clave previamente conocida para codificar y decodificar mensajes.
Una letra en el texto original es reemplazada por otra letra que se encuentra un número fijo de posiciones más adelante en el alfabeto. Por ejemplo, con un desplazamiento de 3, la A sería sustituida por la D (situada 3 lugares a la derecha de la A), la B sería reemplazada por la E, etc. Este método debe su nombre a Julio César, que lo usaba para comunicarse con sus generales. El valor de desplazamiento es la clave del método. En el archivo cesar-subir.rkt se encuentra una implementación incompleta de este método. Se pide completar las definiciones faltantes. Puede además diseñar todas las funciones auxiliares que crea conveniente.
(define ALFABETO "ABCDEFGHIJKLMNÑOPQRSTUVWXYZ 0123456789") (define CLAVE 3) (define CODIGO-DEL-CESAR (cifrado CLAVE ALFABETO))
y evaluamos las siguientes expresiones
(encriptar-mensaje "HOLA" ALFABETO CLAVE) (encriptar-mensaje "ATACAR A LAS 18" ALFABETO CLAVE) (encriptar-mensaje "LA OPERACION ES REVERSIBLE" ALFABETO CLAVE) (desencriptar-mensaje (encriptar-mensaje "LA OPERACION ES REVERSIBLE" ALFABETO CLAVE) ALFABETO CLAVE)
obtenemos
"KRÑD" "DWDFDU2D2ÑDV24B" "ÑD2RSHUDFLRP2HV2UHYHUVLEÑH" "LA OPERACION ES REVERSIBLE"